Climbing Stairs

Today, we’ll talk about the classic climbing stairs problem.

You are climbing a staircase. It takes n steps to reach the top.

Each time you can either climb 1 or 2 steps. In how many distinct ways can you climb to the top?

How do we compose a solution? First, lets see how this solution can initiatively be solved and then see if it is a dynamic programming problem.

Initiative Solution

Let’s start by looking at some simple cases. We will denote the function f(n) as the distinct number of ways to climb to step n.

f(0) = 1
f(1) = 1
f(2) = 2 ([{1, 1}, {2}])

Take a look at f(2) = how many distinct ways can you climb to the 2nd step. We can do this in two ways, by taking 2 1-steps and by taking 1 2-step. Let’s continue. What about f(3)?

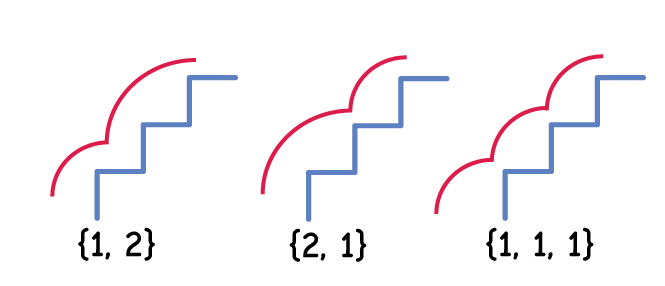
For f(3), we can see the answer is 3. We can either start with 1-step then take a one additional 2-step, start with a 2-step and take one additional 1-step or simply take three 1-steps. It’s important to note, in order to get to the third step, we must be at step 1 (n-2) or step 2 (n-1). This indicates that the maximum number of distinct ways to climb to step 3 must include the number of distinct ways to climb to step n-1 and n-2. We’ll see this more clearly with f(4):

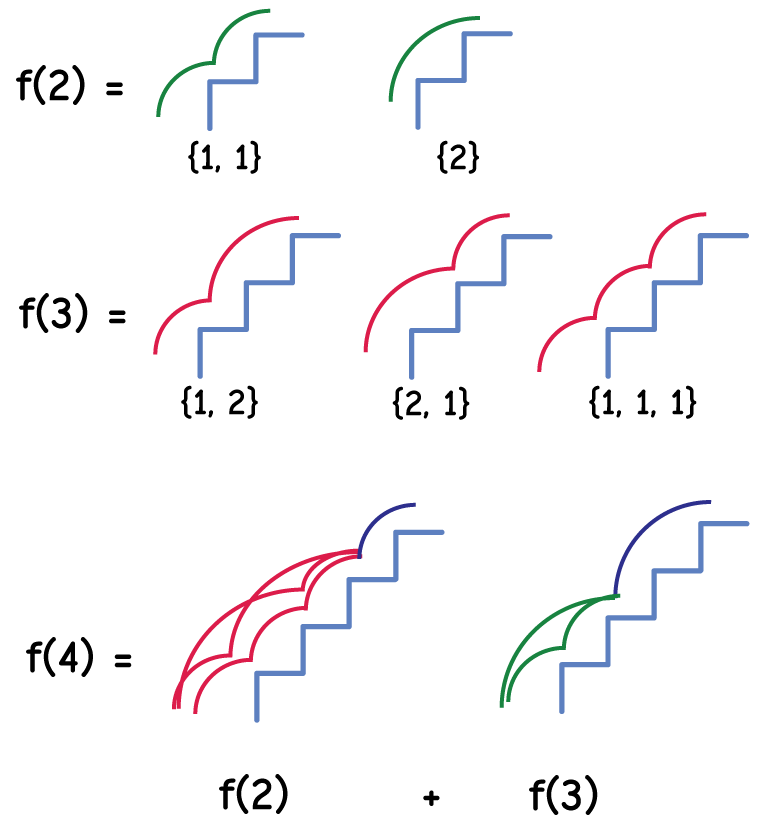
We see from the diagram, that f(4) must include f(3) plus f(2). Because the final step from step 3 and step 2 are different, we can conclude that there are no duplicate paths in all of the paths that make up f(2) + the final 2-step AND all the paths that make up f(3) + the final 1-step.

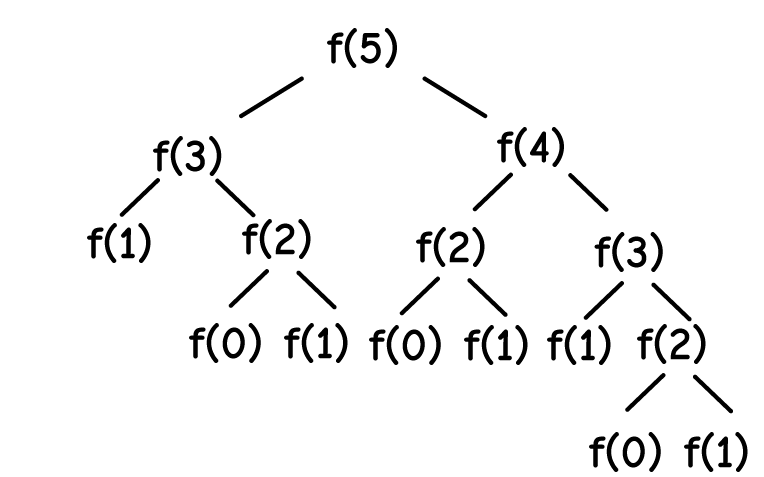
Overlapping Sub-problem – Yes. We can see that as we break the problem down, we are repeating the subproblems multiple times.

Optimal Substructure – Yes. The maximum number of distinct ways to climb to step n is the maximum number of ways to climb to i) climb to step n-1 and take 1 more step plus ii) climb to step n-2 and climb 2 steps.

Base case(s) – the two base cases for this solution is f(0) = f(1) = 1 since there is only 1 way to be at step 0 (the start) and step 1.

DP Table

For our state, we only need a 1-D array where at each position n, we simply need to store f(n) = the maximum number of distinct ways to climb to step n.

Memoization

We can achieve this solution using a top-down memoization technique. We start at f(n) and keep breaking the problem down into sub-problems until we reach our base cases:

class Solution {
    private int[] cache = new int[46];
        
    public int climbStairs(int n) {
        
        if (n==0 || n==1) {
            return 1;
        }
        
        if (cache[n]==0){
            int result = climbStairs(n-1) + climbStairs(n-2);            
            cache[n] = result;            
        }            
        return cache[n];
    }        
}

Note: we know from our problem definition, our cache size needs to be 46. We can be smarter about the size if n was unbounded, but in our case, we want don’t want to add unnecessary complexity.

Tabulation

Using tabulation, we can compute from the bottom-up. I.e. Start at f(1), f(2), f(3)…and so on up to f(n).

class Solution {        
    public int climbStairs(int n) {
        int[] cache = new int[n + 1];
        cache[0] = 1;
        cache[1] = 1;
        
        for(int i=2; i<=n; i++){
            cache[i] = cache[i-1] + cache[i-2];
        }
        return cache[n];                
    }        
}

Conclusion

Though the solution is very simple, the tricky portion is the understanding that f(n) = f(n-1) + f(n-2). While this might be immediately clear to some, it is one of the more common aspects that trick people up.