Coin Change

Today, we’ll analyze the popular interview question coin change.

You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1

We have a infinite number of coins and only need to return the number of coins and not the coins themselves. As usual, let’s denote f(n) be the fewest number of coins required to add up to n.

Optimal Substructure – The fewest number of coins to achieve a sum of n is the most optimal way of to achieve n from a value of n-i where i is one of the coins. In other words, given coins = [1, 2, 5], the most optimal way of achieving f(11):

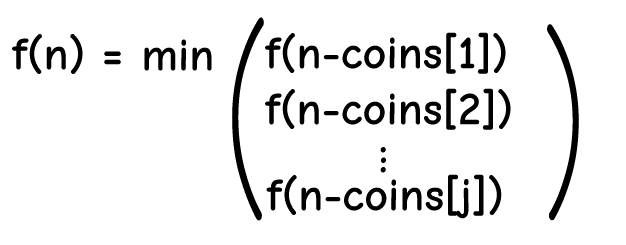
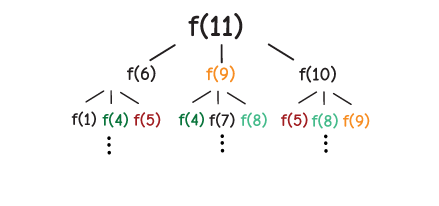
Overlapping Sub-problem – Yes, given the optimal substructure described above, we do have overlapping subproblems. The function call tree clearly shows the number of duplicate calls invoked.

Base Case – The base case is when n=0, f(0)=0.

DP Table

The DP table simply keeps track of the fewest number of coins f(n) in order to reach the sum n. I.e. memo[n] = f(n)

Tabulation

public int coinChange(int[] coins, int amount) {
		if (amount < 0) {
			return -1;
		} else if (amount == 0) {
			return 0;
		}

		int[] memo = new int[amount + 1];
		memo[0] = 0;

		// loop from 0 to amount to fill the array
		for (int i = 1; i <= amount; i++) {
			int minFound = -1;
 
			// loop though all the coins and find the most optimum way of 
			// getting to f(n) using the coins in the coin list 
			for (int j = 0; j < coins.length; j++) {
			    int memoIndex = i - coins[j];
			    
			    if (memoIndex >= 0) {
					int m = memo[memoIndex];
					if ((m > -1 && m < minFound) || minFound == -1) {
						minFound = m;
					}
				}
			}

			if (minFound >= 0) {
				memo[i] = minFound + 1;
			} else {
				memo[i] = -1;
			}
		}
		return memo[amount];
	}

Conclusion

We’ll omit the recursive DP solution since the problem is relatively straight forward.