Unique Paths

Today, we’ll talk about the unique paths problem.

A robot is located at the top-left corner of a m x n grid. The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked ‘Finish’ in the diagram below).

How many possible unique paths are there?

Since at any given position, the user can make 2 decisions, the trivial DFS solution will be O(2ⁿ) Let’s study some interesting facts that might lead us to a better solution.

Fact 1: Since the robot can only move right or down, all coordinates where m = 0 OR n = 0 are 1. This is because there is only one way to reach those coordinates because they are on the edges of the grid.

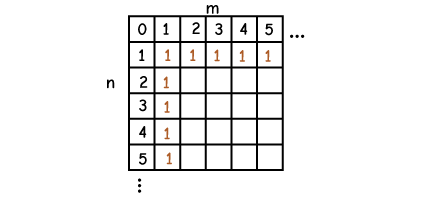
Fact 2: The number of unique paths to a position (m, n) is the number of unique paths to position (m – 1, n) plus the number of uniquely paths from position (m, n – 1). This is (m – 1, n) and (m, n – 1) are the only two grid positions where move in one step to (m, n).

This immediately looks like a dynamic programing problem since we have our base case and optimal substructure properties filled.

Overlapping Sub-problem – Yes. We can see that as we break the problem down, we are repeating the subproblems multiple times. To get an idea why, consider the tree of function invocations.

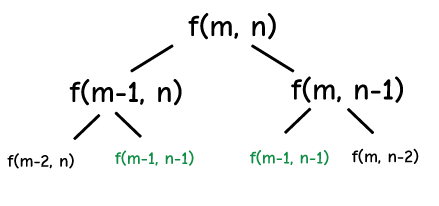
Optimal Substructure – Yes. The optimal solution to f(n) must include the optimal solution to f(m-1, n) and f(m, n-1) otherwise the solution will not be optimal.

Base Case – The base case is when n=0 or m=0 (as mentioned in fact 1).

DP Table

In this problem, our table will be a 2D array of size m by n. Each position (m, n) will hold the maximum number of unique paths to get to (m, n).

Tabulation

class Solution {
    public int uniquePaths(int m, int n) {
    	
    	if (m == 1 && n == 1) {
    		return 1;
    	}
        
        int[][] memo = new int[m][n];
        
        for(int i=0; i<m; i++){
            memo[i][0]=1;
        }
        
        for(int i=0; i<n; i++){
            memo[0][i]=1;
        }
        
        for(int i=1; i<m; i++){
          for(int j=1; j<n; j++){
            memo[i][j] = memo[i][j-1] + memo[i-1][j];
          }  
        }
        
        return memo[m-1][n-1];
    }
}

Conclusion

The unique paths is a fairly straight forward solution with the tabulation method so I’ll omit the recursive memoization method for now.